Révolutions harmoniques : les échelles modulantes

D’autres systèmes tonals alternatifs ?

Jusqu’ici, nous avons montré que l’échelle diatonique et son complémentaire l’échelle pentatonique se prêtaient à la modulation. Au sein de la division de l’octave en 12 parties égales, ces échelles sont-elles les seules possédant cette propriété ?

Une recherche systématique menée avec un ordinateur permet de répondre à cette question. Voici la sortie d’un programme écrit pour l’occasion :

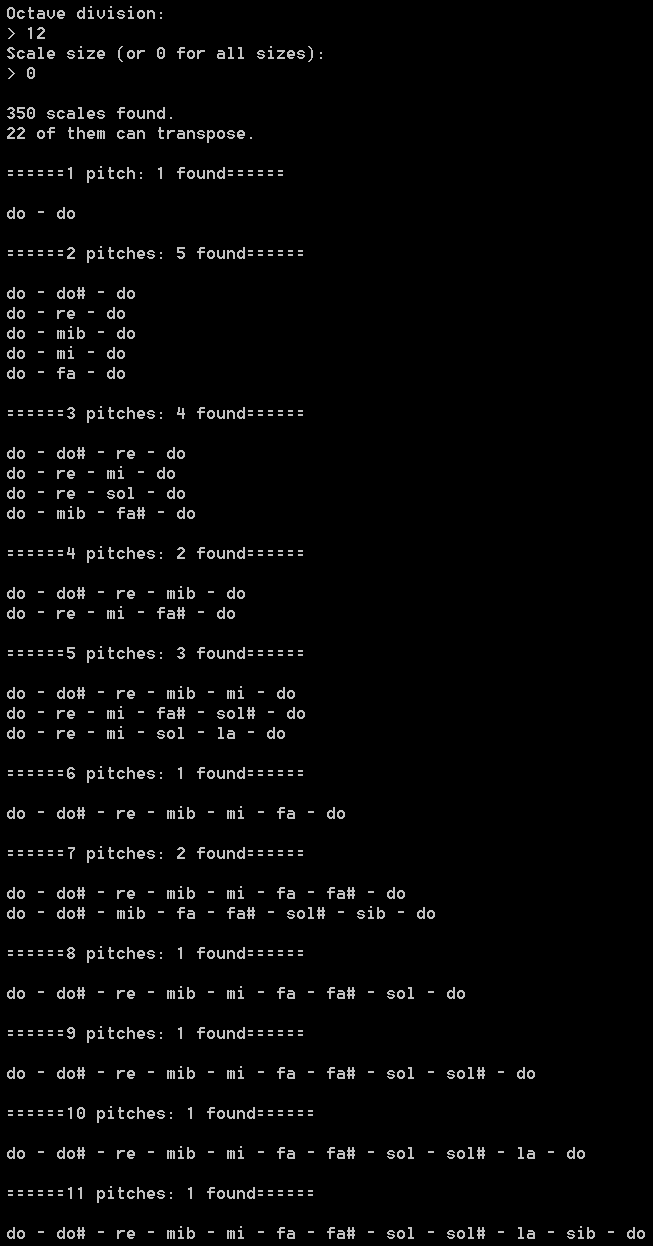
Prenons le temps d’analyser les 22 échelles modulantes obtenues. Pour un meilleur confort de lecture, voici leur écriture en notation musicale :

Commençons par quelques remarques générales :

• Le programme est conçu pour présenter chaque échelle dans une unique configuration. Ainsi, le mode pentatonique, qui apparaît en dernière position des modes à 5 sons, n’est donné que dans la disposition do–ré–mi–sol–la–do (intervalles en demi-tons 2–2–3–2–3), et pas, par exemple, dans sa transposition do–ré–fa–sol–la–do (intervalles 2–3–2–2–3).
• Malgré la remarque ci-dessus selon laquelle si une échelle est modulante, alors son échelle complémentaire l’est aussi, dans la sortie du programme, quelques échelles sont représentées sans que leur complémentaire le soit. En effet, nous avons ajusté l’algorithme pour retirer les échelles dont la modulation nécessiterait de faire se croiser deux notes :

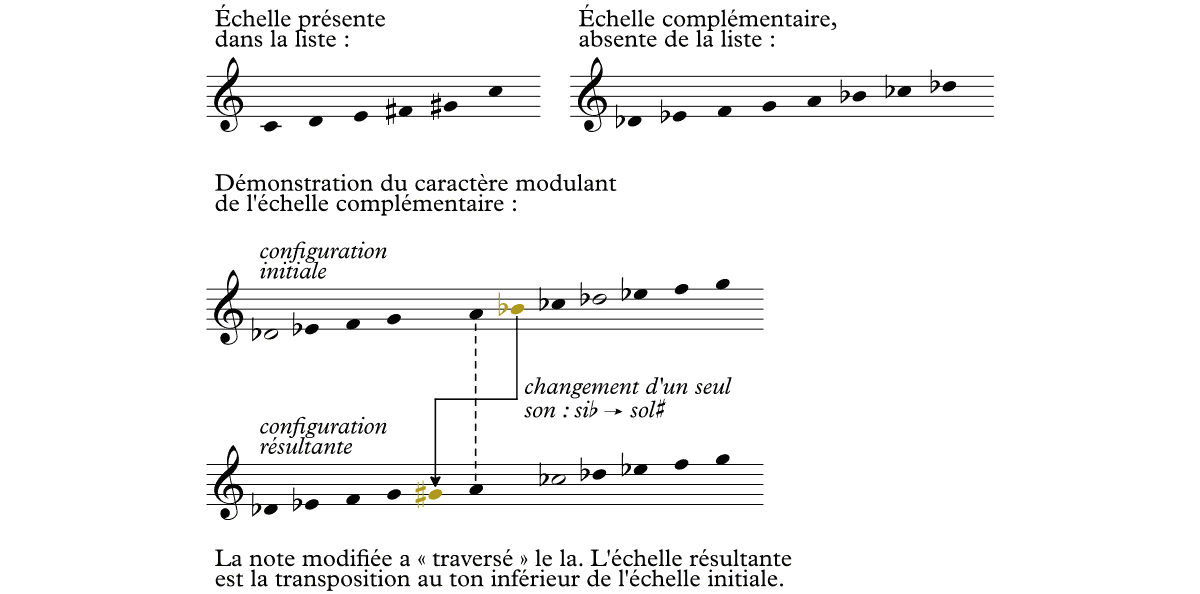
Examinons maintenant en détail les échelles trouvées. Tout d’abord, il y a quelques échelles que les mathématiciens qualifieraient de triviales :

Il est évident que l’échelle du haut, qui ne contient qu’une note, est modulante : on peut librement déplacer la hauteur pour obtenir la même échelle transposée. Toute échelle formée d’un unique intervalle de deux sons (hors triton) est aussi trivialement modulante : on peut déplacer la note du bas au-dessus de la note du haut pour reformer l’intervalle transposé.

Ensuite, on peut remarquer une espèce d’escalier formé par les échelles situées en premier sur chaque ligne :

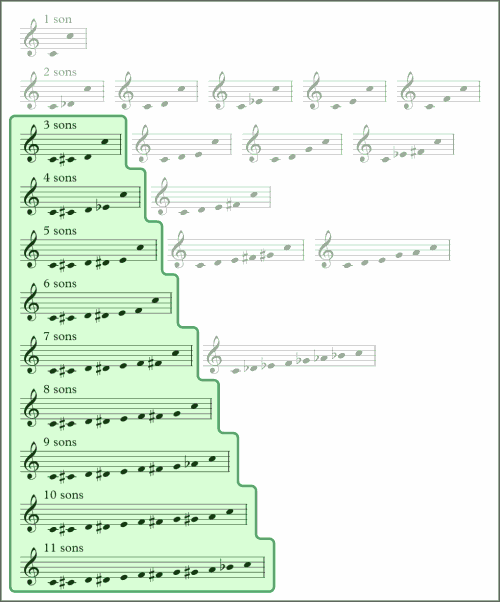
Toutes les échelles de cette zone consistent en une unique série de notes groupées en un paquet chromatique. En termes d’intervalles, ils comportent une succession de demi-tons et un seul grand intervalle. Par exemple, la première échelle de la ligne « 7 sons » parcourt une première quarte augmentée chromatiquement, puis rejoint l’octave en sautant une seconde quarte augmentée d’un seul coup.

Il est facile de voir pourquoi les échelles de ce type sont modulantes : en déplaçant l’une des notes bordant le grand intervalle vide à l’autre extrémité de ce grand intervalle, on obtient une nouvelle échelle chromatique avec un trou de même taille – donc une transposition de l’échelle d’origine. Voici l’opération réalisée sur la première échelle de la ligne « 7 sons », que nous venons de prendre comme exemple :

Puisque ces échelles couvrent seulement une portion de la gamme chromatique, nous pourrions les appeler « échelles oligochromatiques ». Parmi les contraintes sur les échelles exposées auparavant, aucune échelle oligochromatique ne satisfait à la fois à celle de « caractère conjoint » et à celle portant sur le nombre de hauteurs. Ces échelles ont toutefois peut-être des vertus musicales, qui restent à explorer :

• Mélodiquement, elles présentent un grand saut bien reconnaissable. Il est possible de jouer avec les différents intervalles qui enjambent ce fossé de plus ou moins près. Pour les échelles oligochromatiques de 7 à 11 sons, l’intervalle vide caractéristique peut aussi être retrouvé transposé dans la zone chromatique de l’échelle. On peut enfin les utiliser pour définir des modes dont la note principale est située n’importe où dans la séquence en demi-tons.
• Harmoniquement, elles engendrent un cycle de 12 modulations. À part pour l’échelle à 11 sons, contrairement au système tonal habituel, chacune de ces modulations demande de déplacer une hauteur non pas d’un demi-ton mais d’un plus grand intervalle, ce qui peut créer un effet sonore intéressant.

L’extrait sonore suivant fait entendre une série de modulations au sein de ce système. Avec les demi-tons de l’échelle joués simultanément, l’ensemble est dissonant. Le cycle harmonique est bien audible :

Ces premiers cas traités, il reste assez peu d’échelles à examiner. On peut encore isoler les échelles qui viennent en deuxième position sur les lignes « 3 sons », « 4 sons » et « 5 sons ». Ces échelles correspondent à trois sous-ensembles de la gamme par tons :

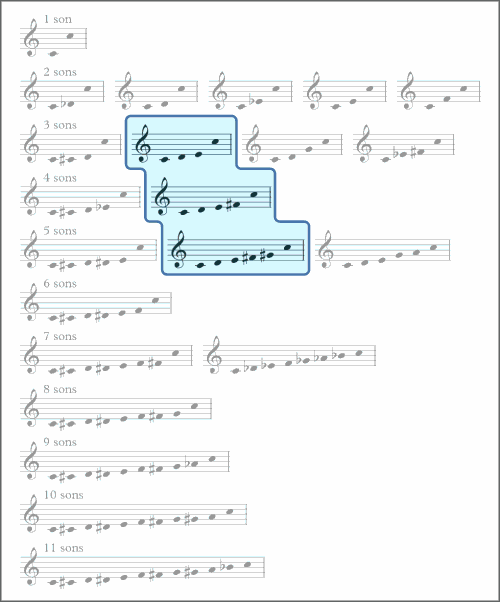
Ce qui suit est un avis subjectif : ces échelles sonnent invariablement comme des appauvrissements de la gamme par tons complète. Voici une tentative de rationalisation de cette impression :

• Mélodiquement, les échelles à 3 et 4 sons offrent très peu de possibilités du fait de leur taille.
• Harmoniquement, ces versions « trouées » de la gamme par tons ne peuvent tirer pleinement parti de leur capacité à moduler. En effet, les modulations laissent l’échelle confinée dans la même gamme par tons, déplaçant seulement la position des notes absentes. Les modulations laissent alors à l’auditeur la sensation de rester dans une gamme par tons fixe, et sont de peu d’effet.

Il est intéressant de noter que le cycle de modulations de ces échelles comporte seulement six paliers : on retrouve la configuration initiale après six modulations successives, contre 12 pour la plupart des autres échelles modulantes.

Il reste encore deux échelles à 3 sons dont nous n’avons pas parlé :

Avec trois sons, il n’est pas question de richesse mélodique. De plus, la seconde échelle (do–mi bémol–fa dièse) souffre du même problème que les sous-ensembles de la gamme par tons : en tant que partie de l’accord de septième diminuée, ses modulations (au nombre de quatre) ne donnent aucune impression de changement harmonique. En revanche, la première (do–ré–sol) fournit par modulations successives une intéressante séquence d’accords, qui met douze transpositions pour revenir à son état initial :

Pour pouvoir s’en faire une idée, voici deux nouveaux extraits musicaux algorithmiques qui exploitent cette étrange marche harmonique. Les modulations se produisent à un rythme deux fois plus lent dans le second extrait que dans le premier. Toutes les voix restent strictement cantonnées aux trois notes de l’échelle.

Cette marche harmonique a une affinité avec le cycle de modulations de l’échelle pentatonique ; en fait, elle en constitue un sous-ensemble.

Enfin, au terme de notre exploration systématique des échelles modulantes dans l’octave à 12 sons, il reste seulement deux échelles :

La première, à 5 sons, est le mode pentatonique des touches noires du piano (ici sous sa forme do–ré–mi–sol–la). La seconde est l’échelle diatonique, celle du mode majeur et des touches blanches du piano, retrouvé par l’algorithme sous la forme du mode locrien (mode de si). Ces deux échelles, déjà traitées ci-dessus et que nous avons volontairement gardées pour la fin de notre tour d’horizon, occupent une place privilégiée dans l’écosystème des 22 échelles modulantes : en effet, ce sont les deux seules parmi ce choix de départ assez vaste qui satisfassent aux critères « nombre de notes » et « caractère conjoint » définis plus haut. De plus, elles vérifient aussi le critère de redondance intervallique, étant toutes deux construites comme des successions de deux intervalles différents alternés de façon légèrement irrégulière (demi-ton et ton pour l’échelle diatonique, ton et tierce mineure pour l’échelle pentatonique).

L’utilisation d’un algorithme nous a donc appris quelques éléments intéressants sur les échelles modulantes au sein de l’octave divisée en demi-tons :

• Il existe une famille d’échelle « oligochromatiques », se prêtant à l’élaboration de systèmes pseudo-tonals, et qui restent à explorer musicalement.
• La recherche systématique d’échelles modulantes peut conduire à la découverte de marches harmoniques originales.
• Les deux échelles qui correspondent respectivement aux touches blanches et aux touches noires des instruments à clavier, et dont l’une est la base du système tonal occidental, doivent probablement leur succès historique à une conjonction de propriétés mathématiques (caractères modulant, nombre de notes adapté, caractère conjoint, redondance intervallique) qui les rend uniques.

Dans la page suivante, nous élargirons notre réflexion à des échelles qui sortent de la division usuelle de l’octave en 12 parties égales.