Antoine Gabriel Brun – Révolutions harmoniques : Les échelles modulantes
Les échelles de notes occidentales, basées sur la division de l’octave en 12 parties égales, réalisent un triple miracle : se chanter facilement, être prodigues en intervalles consonants, et permettre les modulations. Est-il possible, si nous comprenons assez bien ces critères, de produire d’aussi bons systèmes tonals alternatifs ?
Dans cet article : modes et échelles – critères de sélection d’un mode – transposition – divisions de l’octave – systèmes modulants – consonance et dissonance – un autre regard sur les tempéraments – un rendez-vous manqué avec le nombre d’or…
Pourquoi dans un contexte musical donné, l’évolution des styles musicaux finit-elle par privilégier certaines échelles mélodiques plus que d’autres ? Les modes majeur et mineur en occident, les maqamat arabes, les différents modes pratiqués de par le monde, ont-ils été sélectionnés au cours des siècles pour des caractéristiques particulières leur ayant conféré des avantages évolutifs (pour reprendre hors de son contexte le vocabulaire darwinien), ou bien sont-ils les sous-produits fortuits des contraintes en matière de lutherie et de la succession des styles musicaux et des théories harmoniques ?
Cette question, dont la réponse est d’ailleurs probablement fort variable selon les contextes culturels étudiés, ne trouvera aucune réponse définitive ici. Cependant, plusieurs chercheurs d’univers différents s’y sont intéressés, et ont tenté de déterminer si certains critères simples permettaient de comprendre le succès de certains modes plus que d’autres. Le critère dont nous parlerons le plus ici, qui a une importance énorme dans la musique européenne des derniers siècles, est le caractère modulant que présentent certaines échelles.

À propos de ce qui va suivre
Cet article adopte le point de vue du bidouilleur-compositeur, parfois du bricoleur-programmeur. Il n’a aucune prétention ethnomusicologique ni acoustique, et est empreint d’une dose d’ignorance et de subjectivité.
Quelques critères généraux
Supposons que nous souhaitions refonder la théorie musicale sur de nouvelles bases, et que nous commencions par remettre en question nos héritages en ce qui concerne les hauteurs – cette expérience de pensée servant à mieux comprendre les enjeux qui peuvent conduire un compositeur à utiliser une échelle de sons ou une autre.
Armé d’un instrument basique, par exemple une corde unique frottée avec un archet, et débarrassé des préjugés hérités de vos années de solfège ou de ce que vous avez appris lors de votre dernier voyage en Inde, un univers de possibilités infini s’ouvre devant vous. Seule concession : décidons de jouer sur une échelle donnée, plutôt qu’avec des hauteurs non fixées.

Faut-il absolument une échelle ?
Ce choix, pourtant, ne va pas de soi – nous pourrions sans peine concevoir plusieurs alternatives : faire de la musique avec des bruits sans hauteur définie, jouer une musique à dominance rythmique sans égard pour les hauteurs, baser la mélodie sur des glissandos sans aucun point fixe…
Même avec cette contrainte, le nombre de possibilités pour refonder la musique suivant vos goûts en matière de modes semble démesurément grand. Vous pourriez opter pour une musique jouée sur seulement deux sons ; baser toute harmonie et toute mélodie sur les notes accessibles en harmoniques naturelles et les sons situés légèrement en-dessous traités comme des appoggiatures ; ou encore, diviser deux octaves chacune en cinq parties égales, choisir un mode que vous nommerez « mode proto-octo-ortho-euphonique » car après quelques expérimentations vous trouvez qu’il sonne spécialement bien, etc. Voici ce que pourraient donner ces différentes idées, en supposant que votre unique corde soit accordée sur un sol :

Même si absolument tout choix de hauteurs est possible, peut-être y a-t-il tout de même quelques contraintes ou lignes de conduite qu’il serait raisonnable de suivre pour que votre échelle de notes soit la plus intéressante possible ? Voici ci-dessous quelques propositions de critères, que respectent bon nombre de modes traditionnellement utilisés tout autour du monde. Gardons toutefois en tête que chaque critère est plus ou moins subjectif, et qu’il est certainement possible d’exhiber pour chacun de nombreux modes traditionnels qui ne le respectent pas…
Nombre de hauteurs
La plupart des modes issus de la tradition ont entre 5 et 8 hauteurs. En-deçà, on peut considérer que le mode offre peu de possibilités mélodiques et de combinaisons d’intervalles ; au-delà, l’oreille de l’auditeur peut facilement se perdre.

Dans le cadre de votre musique, ces limites haute et basse ne demandent qu’à être franchies. La première pièce de la Musica Ricercata de Ligeti n’utilise que des la à l’exception de la dernière note ; la musique dodécaphonique utilise douze sons divisant également l’octave dans le but d’éviter tout sentiment de hiérarchie entre les hauteurs.
Caractère octaviant
Nombre de modes traditionnels sont octaviants, c’est-à-dire qu’ils se répètent périodiquement à distance d’une octave. Cet intervalle étant pour des raisons physiques la résonance la plus parfaite (après l’unisson), deux notes à l’octaves sont souvent perçues comme identiques ou fortement apparentées ; les échelles de hauteurs tendent donc à reproduire un même schéma à distance d’une octave, et si les notes sont nommées, leur nom est souvent reproduit à l’identique.
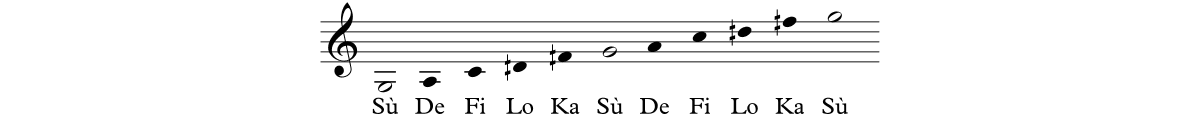
Il n’y a pas d’obstacle majeur à contourner cette contrainte, cependant la répétition du mode à distance d’une octave permet d’en avoir plus facilement une représentation mentale, et surtout engendre automatiquement des musiques bien plus consonantes qu’une autre périodicité (ou que pas de périodicité du tout).
Irrégularité suffisante, non périodicité
Au sein d’une échelle, une ou plusieurs notes peuvent endosser un rôle particulier, harmonique ou mélodique, par exemple finale, appoggiature, bourdon…
La différenciation des rôles est grandement facilitée si l’échelle comporte des points de repère intervalliques bien reconnaissables. Ainsi, un mode qui diviserait l’octave en cinq parties absolument égales se prête moins facilement à l’élaboration d’une hiérarchie au sein du mode qu’une autre échelle qui la divise en cinq parties inégales (dont une ou deux sont plus grandes ou plus petites).
Dans la musique occidentale, les modes sont identifiés par une alternance irrégulière de tons et de demi-tons. Les modes pentatoniques en usage, quant à eux, sont souvent constitués d’une alternance d’intervalles dans des rapports proches de 2:3 (dans la terminologie occidentale, des tons et des tierces mineures).
Rares sont les modes traditionnels qui proposent une division absolument régulière de l’octave. La gamme par tons, qui « découpe » l’octave en six parties égales, a été beaucoup moins utilisée dans la musique occidentale que n’aurait pu le permettre sa simplicité conceptuelle.
De même, les modes qui présentent une périodicité inférieure à l’octave (par exemple une répétition du même motif deux ou trois fois) ont tendance à perdre l’auditeur en quête de repères mélodiques, puisque les mêmes repères auditifs se trouvent à plusieurs endroits de leur série d’intervalles. Ils n’ont eu de succès que dans le cadre de constructions savantes.

Bien sûr, toutes ces limites peuvent être dépassées. La gamme par tons et les autres modes à transposition limitée font ainsi partie intégrante de la musique de plusieurs compositeurs, tels Debussy, Ravel et Messiaen.
Caractère conjoint…
Pour se prêter au chant, et pour être joués sur des instruments à cordes ou à vent, les échelles habituelles tendent à être relativement conjointes. Peu de modes traditionnels comportent des intervalles vides supérieurs à la tierce majeure, un intervalle dont le franchissement répété demande encore peu d’efforts vocaux. Les modes occidentaux remplissent de tons et de demi-tons tous les intervalles supérieurs à la seconde.
…mais aussi suffisamment disjoint
Cependant, les intervalles trop petits posent aussi problème, car il peut être plus difficile de reconnaître à l’oreille des notes très proches ou de concevoir des instruments pouvant les jouer de manière différenciée. Les modes occidentaux ne descendent pas en dessous du demi-ton ; certaines échelles non occidentales présentent de petits intervalles, mais très rarement en grand nombre dans une même échelle.
Redondance intervallique et construction par délétion
Malgré le critère de non périodicité, de nombreux modes présentent des redondances internes, disposées de manière irrégulière au sein de l’octave. C’est le cas par exemple du mode majeur et des modes pentatoniques de rapport 2:3 :

Cet effet est souvent obtenu en utilisant une subdivision régulière de l’octave, puis en conservant seulement certaines notes parmi l’ensemble des hauteurs obtenues. Cette méthode de construction, qui permet de générer à peu de frais des échelles possédant des redondances intervalliques internes, est aussi avantageuse pour la conception des instruments à frettes et des idiophones.

Caractère modulant – L’exemple du mode majeur
Les propriétés citées ci-dessus en guise d’introduction sont semi-universelles : elles s’appliquent plus ou moins bien, se retrouvent dans plusieurs cultures musicales différentes sans pleinement accéder au statut de règles générales, et ont été maintes fois piétinées par toutes sortes de compositeurs occidentaux peu scrupuleux et désireux d’essayer de nouvelles choses.
D’ordre mathématique, la propriété dont il va être question maintenant est encore moins générale, encore plus spécifique à la conception occidentale de la musique et à ses expressions les plus récentes – quelques siècles tout au plus. Elle s’applique à quelques autres modes traditionnels, mais au prix de certaines réserves et certains ajustements. Cependant, il s’agit d’une propriété d’une telle importance qu’elle mérite d’être étudiée avec attention.

Définition
Une échelle peut être qualifiée de « modulante » si en modifiant un seul son, on peut retrouver une version transposée de l’échelle initiale.
L’exemple le plus évident (pour un lecteur occidental et musicien) est celui du mode majeur :

Si une échelle de notes est modulante, il n’y a en fait pas une seule, mais deux notes qui permettent d’effectuer une modulation : l’une avec un déplacement de hauteur ascendant, l’autre avec un déplacement descendant. Ainsi en do majeur, si hausser le fa d’un demi-ton permet de transposer l’échelle d’une quinte vers le haut, abaisser le si du même intervalle permet de la transposer une quinte vers le bas.
La propriété de modulation du mode majeur n’est possible que parce que ce mode respecte déjà certains critères présentés dans la section précédente. Ainsi, pour être modulant, il faut d’abord être octaviant, ne pas avoir de périodicité à l’intérieur de l’octave, et posséder des redondances intervalliques. Cependant, ces critères ne sont pas suffisants pour qu’un mode soit modulant ; en fait, pour une échelle, pouvoir moduler est assez rare.
Le mode majeur a donc une propriété remarquable. Faut-il y voir la raison de son succès historique ? C’est en tout cas la thèse du mathématicien Michel Broué, qui s’est penché sur la gamme classique et a tenté de déterminer, avec des outils mathématiques simples, ce qu’elle avait d’assez extraordinaire pour justifier sa longévité et sa diffusion. Il détaille ses découvertes dans un article passionnant de 2001 intitulé Les tonalités musicales vues par un mathématicien, consultable ci-dessous :
La propriété de modulation ouvre de vastes perspectives compositionnelles. Elle fournit un système qui permet de changer de mode au cours d’une même pièce musicale, tout en conservant un schéma intervallique constant, et avec une seule note à transformer pour changer de ton. Ce système, le système tonal, a fourni le cadre harmonique de la musique occidentale pendant plusieurs siècles.
Majeur vs. diatonique : mode ou échelle ?
Nous avons vu que l’ensemble des sept notes do–ré–mi–fa–sol–la–si possède la propriété d’être modulant, c’est-à-dire que sur cette échelle, transposer à la quarte ou à la quinte demande de modifier seulement un son :
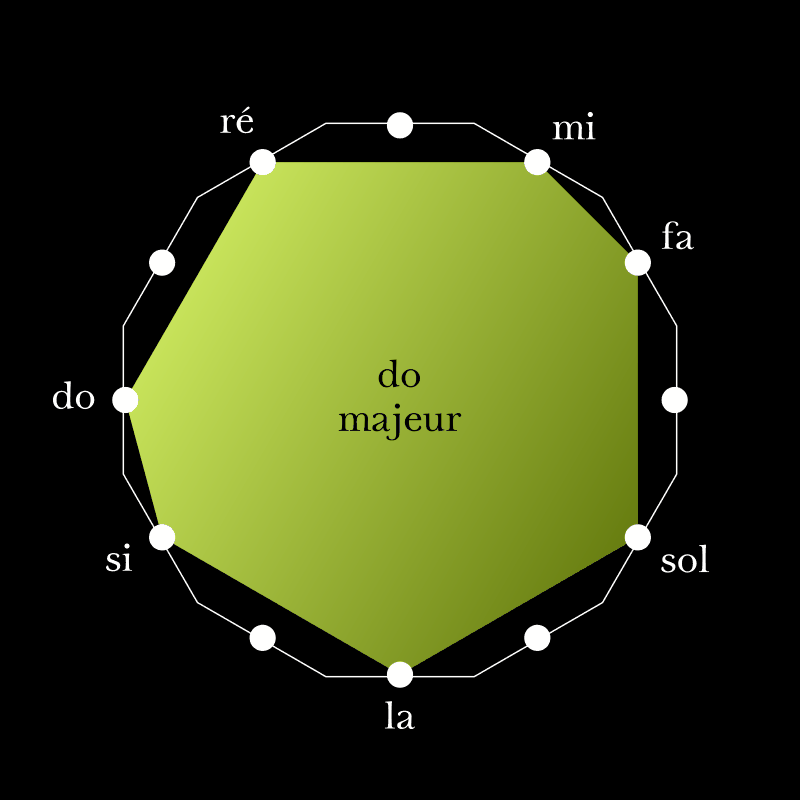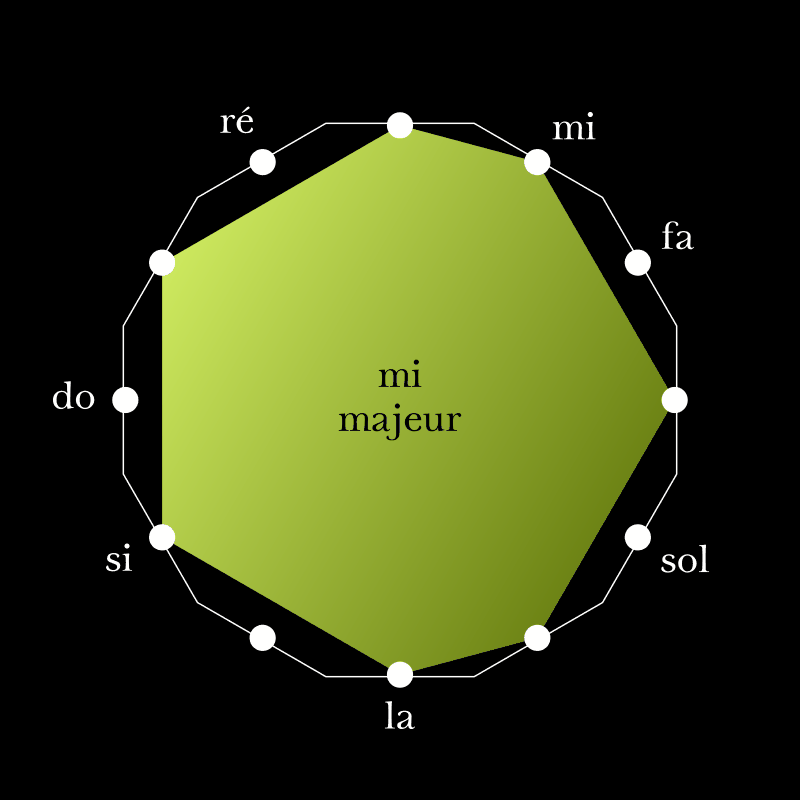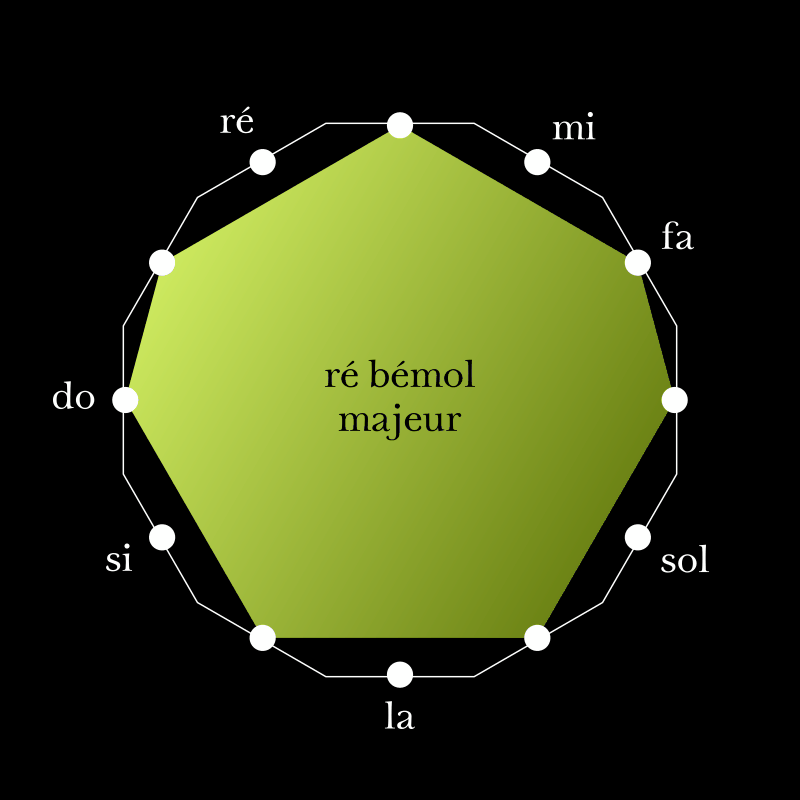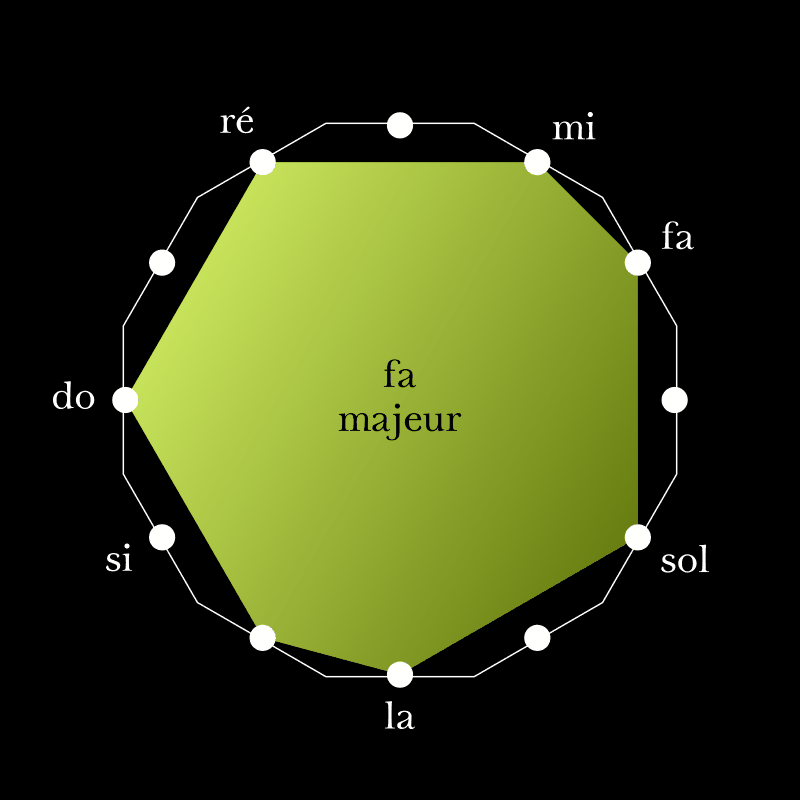
Cette propriété appartient à l’échelle do–ré–mi–fa–sol–la–si, c’est-à-dire à cet ensemble de hauteurs. Elle reste vraie si l’on choisit de faire commencer le mode utilisé sur une autre note que le do.

Mode ou échelle
Employés indifféremment jusqu’ici, ces deux mots n’ont pas tout à fait la même signification. Une échelle de notes désigne simplement un ensemble de hauteurs que l’on utilise dans une mélodie ou une harmonie. Un mode correspond aussi à un ensemble de hauteurs, mais dans lequel certaines notes prennent un rôle particulier (tonique, finale mélodique, dominante, note de passage, appoggiature, degré mobile, etc.)
La série de notes do–ré–mi–fa–sol–la–si dont il est ici question est certes une échelle, mais elle peut être employée comme un mode dans le cadre de la musique tonale. Le do y prend alors le rôle de tonique, et les notes y assurent des fonctions définies (le si a tendance à se résoudre sur le do dans les mélodies, le sol devient dominante, etc.)
Comme le caractère modulant appartient à l’échelle elle-même, tous les modes pouvant être construits sur l’échelle do–ré–mi–fa–sol–la–si peuvent se prêter à la construction d’un système tonal alternatif.
C’est le cas, en particulier, pour les modes « diatoniques » (modes dorien, phrygien, etc.) obtenus en choisissant une note de référence parmi ces sept hauteurs. Ainsi, un système tonal autorisant les modulations peut tout à fait être construit en prenant pour base, par exemple, les douze modes lydiens :

Vous pouvez vérifier ci-dessus que dans ce « système tonal » alternatif, la modulation vers le haut du cycle s’obtient en montant la tonique d’un demi-ton, et la modulation vers le bas en abaissant le quatrième degré d’un demi-ton.
Un système tonal de substitution peut ainsi être construit sur chacun des six modes diatoniques autres que le mode ionien (mode majeur).
Échelle complémentaire et modes pentatoniques
Par sa rare faculté à moduler, l’échelle diatonique (do–ré–mi–fa–sol–la–si) est une exception parmi les modes construits comme des sous-ensembles de la division de l’octave en 12 parties. Est-elle pour autant la seule à posséder cette propriété ?
Le caractère modulant d’une échelle a une particularité étonnante : il se transmet à l’échelle complémentaire.

Échelle complémentaire
Étant donnée une échelle de notes, l’échelle complémentaire est celle composée de toutes les notes absentes de l’échelle initiale.
Par exemple, le complémentaire de l’échelle do–ré–mi–fa–sol–la–si (touches blanches du piano) est l’échelle do dièse–ré dièse–fa dièse–sol dièse–la dièse (touches noires).
Pour formuler autrement la règle énoncée ci-dessus, si une échelle a la capacité de moduler, c’est aussi le cas de son échelle complémentaire.
Explication
Si une échelle E est modulante, alors il existe une note a de E qui, si elle est remplacée par la note b absente de E, transforme E en une version transposée d’elle-même, que l’on peut noter t(E).
Comme E contient a mais pas b, l’échelle complémentaire E′, à l’inverse, contient b mais pas a. Dans E′, il suffit de changer la note b en a pour obtenir t(E)′, le complémentaire de la version transposée de E.
Or, t(E)′ est aussi t(E′) (le complémentaire de l’échelle transposée est aussi la transposition de l’échelle complémentaire). En changeant une seule hauteur, nous avons obtenu une version transposée de E′ : le complémentaire de E est donc aussi modulant.
Le complémentaire de l’échelle modulante do–ré–mi–fa–sol–la–si est l’échelle pentatonique des touches noires du piano. Nous pouvons donc maintenant affirmer que cette configuration scalaire est elle aussi modulante, et peut servir de base à un système tonal :

Voici ci-dessous deux extraits sonores générés grâce à des procédés algorithmiques. Ils permettent d’entendre l’effet de modulations répétées au sein de ce système tonal pentatonique. Les deux extraits présentent un grand nombre de modulations successives, le premier joué par un orchestre synthétique, le second réalisé avec des sons électroniques. Dans les deux cas, l’échelle est traitée de manière amodale, comme un simple réservoir de notes. Les modulations ont lieu à intervalle régulier, sont orientées vers le haut, et parcourent tout le « cycle des quintes » de ce système tonal alternatif. Les deux extraits sont évolutifs : uniquement harmoniques au début, ils font ensuite apparaître des éléments mélodiques.

Écoute au casque
Les exemples musicaux de cet article sont destinés à faire entendre des différences fines, parfois imperceptibles, entre plusieurs échelles pour la plupart originales. Ils sont harmonisés sur une large plage de fréquence et en stéréo. Une écoute au casque, ou avec de bonnes enceintes, est celle qui permet le mieux d’en profiter.
Pourquoi utiliser des procédés algorithmiques ?
Dans cet article, je présente de nombreux extraits sonores destinés à écouter telle ou telle échelle. Je pense en effet qu’un exposé sur les échelles modulantes ne peut être utile qu’accompagné d’exemples permettant de se rendre compte de l’effet auditif que chacune produit. Or, étant donnée la difficulté de générer de la musique dans des modes alternatifs avec des instruments et des logiciels uniquement prévus pour les notes en demi-tons, peu de lecteurs s’y essaieraient par eux-mêmes.
Le but n’est pas de disposer d’une pièce musicale complète écrite en utilisant chaque échelle, mais d’avoir un extrait minimal permettant de se familiariser avec chacune.
J’ai donc mis au point des algorithmes générant automatiquement des contenus musicaux sur différents échelles, en restant aussi neutre et générique que possible. En général, les extraits sont simples et répétitifs ; ils comportent des notes tenues sur les hauteurs de l’échelle, un nuage de notes brèves aléatoires qui remplissent l’harmonie, et parfois des mélodies aléatoires.
Ce choix est aussi pragmatique : il m’a permis de fournir de nombreux exemples musicaux sans avoir à composer une nouvelle pièce à chaque fois.
Dans la page suivante, nous réfléchirons à la possibilité de trouver de nouvelles échelles permettant de réaliser des modulations.

